Fra le tecniche di previsione una di quelle più conosciute è quella dell’analisi delle serie temporali. All’interno di esse prenderemo il modello ARIMA. ARIMA presuppone che i dati da processare abbiano la caratteristica di stazionarietà. È un modello previsionale che si basa sul concetto di regressione, un metodo di approssimazione relativamente intuitivo e di facile interpretazione. ARIMA permette inoltre di avere una misura dell’errore previsionale, elemento essenziale per una trattazione di tipo quantitativo. Per la trattazione dell’argomento si farà uso del software di programmazione Python in ambiente Jupiter Notebook.
Come seguito all’articolo introduttivo sul Machine Learning per il trading (vedi numero 01 di gennaio 2022), analizzeremo qui un primo algoritmo previsionale su fenomeni che variano nel tempo ovvero le Serie Temporali.
Trading basato su Serie Temporali (Time Series)
Alla base delle Serie Temporali c’è il concetto per cui, sotto certe condizioni (stazionarietà) il futuro comportamento di un certo fenomeno è la funzione del comportamento che ne ha caratterizzato il passato. L’analisi delle serie temporali è usata per determinare un buon modello che può essere usato per prevedere le metriche del business come le vendite, il fatturato e, come vedremo i corsi del mercato azionario. La stazionarietà è piuttosto intuitiva ed è una proprietà invariante che significa che le caratteristiche statistiche della serie temporale non cambiano nel tempo. In parole povere, una serie temporale è stazionaria se il suo comportamento non cambia nel tempo. Una tendenza o un ciclo non sono stazionari. Così il compito di previsione diventa, in sostanza, un’attenta analisi del passato più un presupposto che gli stessi modelli e relazioni si manterranno nel futuro. La stazionarietà di una serie è determinata dall’osservazione grafica e nei casi in cui essa risulti non immediata possiamo utilizzare delle tecniche per testarne questa caratteristica (Dickey-Fuller test). Quando le nostre Serie Temporali non sono stazionarie possiamo comunque operare delle trasformazioni sulla stessa serie di dati in modo da renderli stazionari (guardare la trasformata di Fourier per gli intenditori).
La programmazione di un sistema previsionale
Ricordiamo i passi per la programmazione di un codice Machine Learning:
1. Importazione dati
2. Elaborazione e organizzazione dati
3. Definizione del modello da utilizzare
4. Addestramento del modello
5. Valutazione dell’affidabilità del modello
6. Previsione
Utilizzando Python, durante il processo avremmo bisogno di importare le librerie necessarie per le operazioni matematiche, la manipolazione della struttura dei dati, la visualizzazione grafica e a seconda del modello che vogliamo implementare le librerie per gli algoritmi di regressione, di reti neurali, NLP, ed in questo caso ARIMA. Le librerie più diffuse e adatte al nostro scopo possono essere importate digitando le seguenti istruzioni:
import numpy as np import pandas as pd import matplotlib.pyplot as plt from plotly.graph_objs import graph_objs %matplotlib inline from matplotlib.pylab import rcParams rcParams[‘figure.figsize’] = 10,6
Ora passiamo all’importazione dei dati su cui vogliamo fare le nostre previsioni. Per questo ho scelto di analizzare i valori di chiusura giorna-lieri del Volatility Index. Il Volatility Index è più comunemente conosciuto con il suo simbolo di ticker ed è spesso indicato semplicemente come “VIX”. È stato creato dal Chicago Board Options Exchange (CBOE) ed è mantenuto da Cboe Global Markets. Il Cboe Volatility Index (VIX) è un indice in tempo reale che rappresenta le aspettative del mercato per la forza relativa delle variazioni di prezzo a breve termine dell’indice S&P 500 (SPX). La scelta di prevedere l’andamento del VIX è dettata dal fatto che il VIX rispetto alle azioni o agli indici azionari non ha una tendenza specifica ma ha, nella sua natura intrinseca di non stabilità, un comportamento più stazionario.
L’importazione dei dati può essere fatta scaricando un’altra libreria che permette l’estrapolazione dei dati dal sito web yahoo finance e richiamare l’istruzione per poterli importare nel nostro ambiente di programmazione. Assegneremo la serie di dati ad una variabile che chiameremo “data”.
pip install yfinance
data = yf.download(tickers=’^VIX’, period=’1y’, interval=’1d’)


A questo punto potremmo avere la visualizzazione dei dati in forma tabellare o in forma grafica (vedi figura 1 e figura 2)
Impostiamo alcune semplici operazioni sul set di dati a disposizioni in modo da avere solamente solo la Colonna “Date” e “Close” con cui l’algoritmo ARIMA può lavorare.
ARIMA
ARIMA, abbreviazione di “Auto Regressive Integrated Moving Average” è in realtà una classe di modelli che elabora previsioni di una data serie temporale sulla base dei suoi valori passati. Qualsiasi serie temporale a carattere “Stazionario” può essere processata con modelli ARIMA. Un modello ARIMA è caratterizzato da 3 termini: p, d, q dove, p è l’ordine del termine AR q è l’ordine del termine MA d è il numero di differenziazioni necessarie per rendere stazionaria la serie temporale.s Salteremo ulteriori approfondimenti sull’ARIMA per evitare di riportare una lunga trattazione ma invitiamo gli interessati ad approfondire l’argomento per una migliore consapevolezza.
Per Implementare ARIMA ancora abbiamo bisogno di librerie specifiche per le sue operazioni che andiamo a richiamare con le seguenti linee di codice:
from statsmodels.tsa.stattools import acf,
pacf from statsmodels.tsa.arima_model import ARIMA
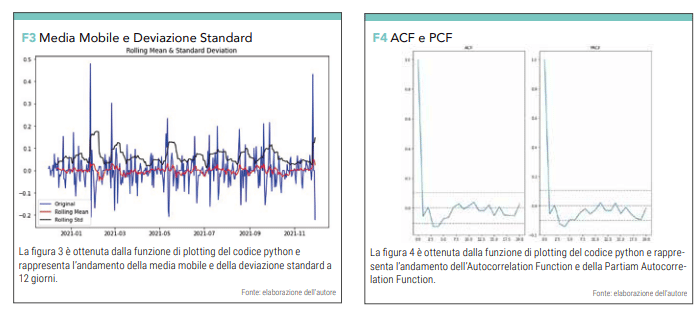
A questo punto implementiamo poche righe di codice che ci permetteranno di visualizzare l’andamento della media mobile a 12 giorni del VIX e l’andamento della sua deviazione standard (vedi figura 4).
rolling_mean = timeseries.rolling(window=12). mean()
rolling_std = timeseries.rolling(window=12).std()
orig = plt.plot(timeseries, color=’blue’,
label=’Original’) mean = plt.plot(rolling_mean, color=’red’,
label=’Rolling Mean’) std = plt.plot(rolling_std, color=’black’,
label=’Rolling Std’) plt.legend(loc=’best’) plt.title(‘Rolling Mean & Standard Deviation’) plt.show()
Con il seguente blocco otteniamo i grafici ACF (Autocorrelation Function) e PCF (Partial Autocorrelation Function) (vedi figura 4). Questa informazione ci dà una indicazione della correlazione di ogni riga di dato (Colonna “Date” e Colonna “Close”) con le righe precedenti. I valori ACF e PCF che incrociano il livello 0 del grafico determinano rispettivamente i parametri p e q, necessari al modello ARIMA.
def plot_acf_dcf():
# ACF and PACF plots lag_acf = acf(dataset_log_first_order_diff, nlags=20) lag_pacf = pacf(dataset_log_first_order_diff, nlags=20, method=’ols’)
# Plot ACF
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0, linestyle=’–‘, color=’gray’) plt.axhline(y=-1.96/np.sqrt(len(dataset_log_first_ order_diff)), linestyle=’–‘, color=’gray’) plt.axhline(y=1.96/np.sqrt(len(dataset_log_first_ order_diff)), linestyle=’–‘, color=’gray’) plt.title(‘ACF’)
# Plot PACF
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0, linestyle=’–‘, color=’gray’) plt.axhline(y=-1.96/np.sqrt(len(dataset_log_first_ order_diff)),linestyle=’–‘, color=’gray’)
plt.axhline(y=1.96/np.sqrt(len(dataset_log_first_ order_diff)), linestyle=’–‘, color=’gray’) plt.title(‘PACF’) plt.tight_layout() plt.show()
A questo punto lanciamo l’algoritmo ARIMA facendo eseguire il codice con p=1, q=1 e d1 =1
def model_ARIMA(indexed_data_log_scale, dataset_log_first_order_diff): #ARIMA Model with p,d,q=1 model = ARIMA(indexed_data_log_scale, order=(1, 1, 1))
results_ARIMA = model.fit(disp=-1) plt.plot(dataset_log_first_order_diff) plt.plot(results_ARIMA.fittedvalues, color=’red’) plt.title(‘RSS: %.4f’% sum((results_ARIMA.fittedvalues-dataset_log_first_order_diff[‘Close’])**2)) plt.show()
return results_ARIMA
All’interno di queste righe di codice è possibile notare la citazione del parametro ‘RSS’ (Residual Sum of Squares) che misura l’errore della previsione.
Come abbiamo già affermato, parte integrante di una previsione quantitative è la misurazione del suo errore. Con l’utilizzo del Dickey-Fuller test2 verifichiamo il carattere stazionario della serie temporale del VIX. Il Dickey-Fuller test è disponibile nella libreria che importiamo allo scopo:
from statsmodels.tsa.stattools import adfuller
Lanciamo adesso la computazione con il blocco:
print (‘Result of Dicky=Fuller Test’)
dftest = adfuller(timeseries[‘Close’], autolag=’AIC’) dfoutput = pd.Series(dftest[0:4], index=[‘Test Statistic’, ‘p-value’, ‘#Lags Used’, ‘#Observations Used’])
for key, value in dftest[4].items(): dfoutput[‘Critical Value (%s)’%key] = value print (dfoutput)
che darà l’output visibile in figura 5.
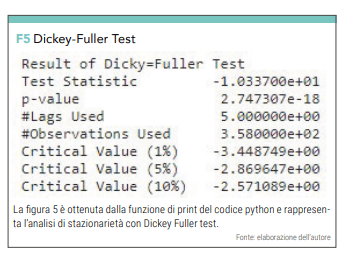
Avendo constatato che il P Value è <0,005 non abbiamo la necessità di trasformare la serie di dati per migliorarne la stazionarietà e siamo pronti a lanciare il codice che ci permette di avere la previsione dei prossimi 30 giorni (da notare il parametro 395 = 365 + 30) che vogliamo.
results_ARIMA = model_ARIMA(indexed_data_log_ scale,dataset_log_first_order_diff)
results_ARIMA.plot_predict(1,395) plt.show()
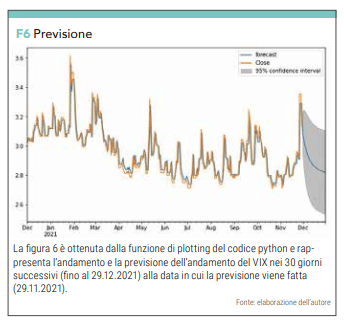
in figura 6 abbiamo l’output grafico mentre il valore numerico ci viene da un array restituito dalle seguenti istruzioni :
futureforecast2 = results_ARIMA.forecast(steps=30) new= np.exp(futureforecast2[0])
print (new)
che vediamo in figura 7.

Conclusioni
Con quanto illustrato non si pretende di dare al lettore uno strumento di decisione per i suoi investimenti. L’utilizzo di questi strumenti per trading reale richiede una conoscenza dell’argomento molto più profonda. Ci limitiamo in questo breve articolo ad illustrare un punto di partenza per approcciare l’intelligenza artificiale e l’applicazione di tecniche di machine learning. Per chi fosse interessato ad ottenere il codice completo e strutturato per un plug and play in ambiente Jupiter Notebook, richiedetelo pure all’autore all’indirizzo email nicola.matarese73@gmail.com. Nei prossimi numeri illustrerò altri algoritmi previsionali che da confrontare di volta in volta con i precedenti.
Note
1 d è il numero di differenziazioni necessarie per rendere stazionaria la serie temporale. Invitiamo il lettore ad approfondire la trattazione.
2 Il test ADF è un comune test statistico utilizzato per verificare se una data serie temporale è stazionaria o meno. È uno dei test statistici più comunemente usati quando si tratta di analizzare la stazionarietà di una serie: https://otexts.com/fpp2/stationarity.html Utilizza le seguenti ipotesi nulle e alternative: H0 : La serie temporale è non stazionaria. In altre parole, ha una struttura dipendente dal tempo e non ha una varianza costante nel tempo. HA : La serie temporale è stazionaria. Se il valore p del test è inferiore a un certo livello di significatività (ad esempio meno del 5%), allora possiamo rifiutare l’ipotesi nulla e concludere che la serie temporale è stazionaria.
Nicola Matarese
 Classe 1973, ha conseguito una laurea magistrale in ingegneria meccanica ed ha ricoperto ruoli manageriali all’interno di realtà industriali in ambito aerospazio e difesa. È appassionato di trading e opera sui mercati dal 2001. Da qualche anno lavora a sistemi di trading supportati da teorie sui Big Data e Intelligenza Artificiale.
Classe 1973, ha conseguito una laurea magistrale in ingegneria meccanica ed ha ricoperto ruoli manageriali all’interno di realtà industriali in ambito aerospazio e difesa. È appassionato di trading e opera sui mercati dal 2001. Da qualche anno lavora a sistemi di trading supportati da teorie sui Big Data e Intelligenza Artificiale.



