Trading Algoritmico
Negli articoli precedenti abbiamo analizzato l’algoritmo ARIMA per elaborare una previsione dell’andamento del CBOE Volatility Index. Come abbiamo visto il VIX ha delle caratteristiche intrinseche di stazionarietà che permettono l’utilizzo delle Serie Temporali direttamente sui valori dell’indice. In questo articolo invece andremo ad analizzare l’indice S&P500 con 2 nuovi algoritmi: AUTOARIMA e ARCH. Il primo è una semplificazione del metodo ARIMA già visto mentre il secondo ci aiuta a studiare, anzichè il trend (e quindi i valori giornalieri dell’indice S&P500), la sua “volatilità” (ovvero la variazione dei valori del giorno dopo). Per la trattazione dell’argomento si farà uso del software di programmazione Python in ambiente Jupiter Notebook.
Premessa
La programmazione di codici di machine learning prevede oltre che una profonda conoscenza dei linguaggi di programmazione anche una notevole comprensione di modelli statistici e matematici. Vista la complessità degli argomenti è bene che il lettore sia consapevole dell’impossibilità di trovare spiegazioni esaurienti su tutta la teoria alla base della trattazione. Rinunciando a questo tuttavia siamo in grado di presentare le potenzialità dell’argomento in poche pagine di testo. Tanto riteniamo sia comunque sufficiente a stimolare la curiosità di coloro che da questo piccolo spunto possano partire e approcciare i mercati con altre metodologie quantitative.
Autoarima
La previsione delle serie temporali è un argomento caldo che ha molte applicazioni possibili, come la previsione del tempo, la pianificazione aziendale, l’allocazione delle risorse e molte altre. Come alternativa al metodo ARIMA visto nel numero precedente, il metodo AUTOARIMA ci permette di determinare automaticamente la migliore combinazione dei valori p, q e d necessari alla costruzione del modello.
Seguendo il solito principio di costruzione di un codice di machine learning[1], partiamo con l’importazione delle librerie di gestione tabelle e grafica.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
STEP 1 – IMPORTAZIONE E LETTURA DATI
Procediamo con l’impostazione delle funzioni che ci permettono di leggere i valori degli ultimi due anni dell’S&P500, quelli che vogliamo analizzare e utilizzare per l’addestramento del modello e le future previsioni:
pip install yfinance
data = yf.download(tickers=‘^GSPC’, period=‘2y’, interval=’1d’)
STEP 2 – ELABORAZIONE, TRASFORMAZIONE E ORGANIZZAZIONE DATI
In questa fase trasformiamo i dati in maniera tale che gli stessi possano essere gestiti dall’algoritmo AUTORIMA. Per esempio, eliminiamo le colonne che non ci servono, sostituiamo i valori nulli dei weekend e dei giorni di festa con i valori dell’ultimo giorno precedente in cui il mercato era aperto.
cols_to_keep = [“Close”]
data = data.loc[:,cols_to_keep]
closingdata = data
closingdata[“week”] = closingdata.index.isocalendar().week
idx = pd.date_range(closingdata.index[0], closingdata.index[–1])
completedata =closingdata.reindex(idx, fill_value= float(“NaN”))
completedata = completedata.fillna(method=‘ffill’)
completedata
L’ultima riga di codice ci darà la possibilità di visualizzare la nuova struttura dati (vedi figura 1).
STEP 3 – DEFINIZIONE DEL MODELLO
Importiamo adesso la libreria che ci permetterà di implementare l’algoritmo AUTOARIMA ed eseguire le operazioni per esso necessarie con le seguenti istruzioni.
!pip install pmdarima
from sklearn.metrics import mean_squared_error
import pmdarima as pm
from pmdarima.arima import auto_arima
STEP 4 – ADDESTRAMENTO DEL MODELLO
Per l’addestramento del modello dobbiamo innanzitutto definire quelli che chiamiamo Data Test Set (i valori che facciamo finta di non conoscere) e Data Train Set (i valori che utilizziamo per addestrare il modello), tra loro complementari, rispettivamente variabili dipendenti e variabili indipendenti, ricavati dalla separazione della totalità dei dati ottenuti alla fine dello Step 1:
number_of_weeks_testing = 4
testdata = completedata.iloc[–number_of_weeks_testing*7:]
traindata = completedata.iloc[:–number_of_weeks_testing*7]
dove testdata partono dal 29.01.2020 e arrivano fino al 31.12.2021 e traindata partono dal 01.01.2022 fino al 28.01.2022.
Procediamo adesso con l’addestramento inserendo il comando:
arima = auto_arima(traindata[“Close”], error_action=‘ignore’, trace=True,
suppress_warnings=True, maxiter=30,
seasonal=True, m=7 [2])
A questo punto AUTOARIMA farà tutte le iterazioni indicate (fino ad un massimo di 30) e determinerà la migliore combinazione dei parametri p, q e d, quella per cui il valore AIC (Akaike information criterion) risulti minimo (vedi figura 2).
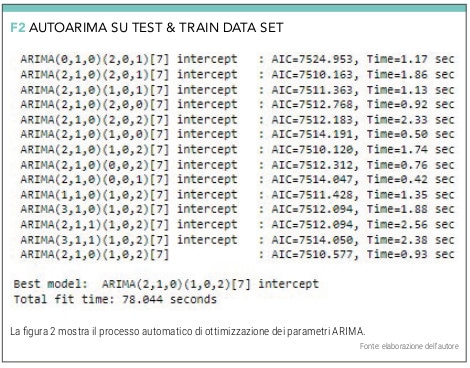
STEP 5 – VALUTAZIONE AFFIDABILITÀ DEL MODELLO
Ora andiamo a far girare le line di codice che ci permettono di ottenere i test data e capire quanto essi si discostino dai valori reali. Calcoliamo pertanto la bontà del modello andando a calcolare lo scarto quadratico medio tra quello che il modello ha previsto (test data) e quali sono effettivamente i dati storici.
performance_collector=[]
for w in range(number_of_weeks_testing):
y_pred = pd.Series(arima.predict(7))
actual = testdata.iloc[w:w+7][“Close”]
performance_collector.append(mean_squared_error(actual,y_pred, squared=False))
print(performance_collector)
print(np.mean(performance_collector))
Lo scarto quadratic medio calcolato è 69.01 (circa l’1,5%).
Se vogliamo anche avere una rappresentazione grafica di quanto il modello è affidabile con il blocco seguente.
plt.title(“S&P500 Predicted data vs Historical data”)
plt.plot(closingdata[‘Close’],label=’Historical Data’)
plt.plot(testdata[‘Close’],label=’Prediction on Test Data’)
plt.xlabel (‘Date’)
plt.ylabel (‘Close’)
plt.legend()
plt.show
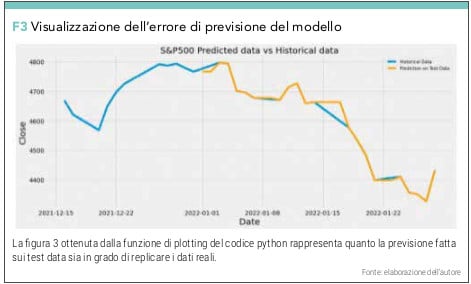
Possiamo stampare e confrontare i valori testdata (Predicted Data) con dati storici fino al 28.01.2022 (Historical Data) con la funzione di creazione grafico (vedi figura 3).
Questo ci serve per capire se e in quale misura il modello che abbiamo costruito può fare buone previsioni. Se il comportamento della previsione (Predicted Data) ricalca bene il dato storico (Historical Data) il modello può essere affidabile anche per previsioni future. È chiaro che se già sappiamo che lo scarto quadratico medio della previsione è dell’1,5% il modello non è ancora ottimizzato per cui dovremmo procedere con quella tecnica che si chiama parametric tuning (cambiamo gli orizzonti temporali, il rapporto tra traindata e testdata, il periodo di osservazione o il numero massimo di iterazioni).
STEP 6 – PREVISIONE
In ogni caso, avendo costruito il modello ed avendo appurato la sua precisione, se accettabile, procediamo con la previsione futura. Per fare questo facciamo girare il modello, non più sui traindata (che arrivano fino al 31.12.2021) ma su tutti i dati (fino al 28.01.2021) indicando come orizzonte di previsione 7 giorni.
fulldata=pd.concat([traindata,testdata],axis=0)
arima = auto_arima(fulldata[“Close”], error_action=‘ignore’, trace=True,
suppress_warnings=True, maxiter=30,
seasonal=True, m=7)
e determiniamo il vettore previsionale con il comando
futureforecast=arima.predict(7[3])
futureforecast
che vediamo in F4.
Operando alcune trasformazioni e utilizzando le funzioni di plotting
plt.title(“S&P500 PREDICTION FOR THE NEXT 7 DAYS WITH AUTOARIMA MODEL”)
plt.xlabel (‘Date’)
plt.ylabel (‘Close Price USD ($)’)
plt.plot(pastandforecast[‘Close’],label=’Historical Data’)
plt.plot(pastandforecast[‘Forecasted_Close’],label=’AUTOARIMA forecast’)
plt.legend()
plt.show
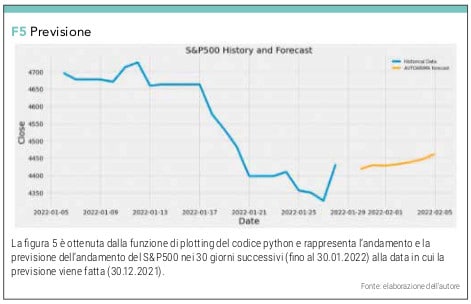
possiamo avere il grafico in figura 5.
ARCH
La logica dietro una previsione fatta sulla base di una serie temporale è quella per cui il valore da prevedere è uguale all’ultimo valore disponibile. In pratica il panettiere che voglia lanciare la produzione di pane per domani può basarsi sulla vendita di oggi. Questa è l’idea di base di un modello di autoregressione di livello 1 (indicata anche con AR 1). A meno di un certo errore la nostra previsione sarà così determinata.
Banalmente se noi conoscessimo questo errore di previsione a priori saremo in grado di fare una previsione con piena certezza. Nel momento in cui aggiungiamo un termine che tiene in considerazione anche delle vendite di pane del giorno precedente (di ieri), possiamo dire che il valore delle vendite di ieri, più l’errore di previsione di ieri (che darebbe la previsione di oggi), più l’errore di oggi, darebbe la previsione di domani. Con questo modello passiamo da un semplice modello AR ad un modello ARMA (auto regressive moving average).
Quello che chiamiamo ARCH (Autoregressive Conditional Heteroskedasticity) è invece un modello che lavora sulla volatilità ovvero sulla differenza del valore di oggi e il valore di ieri. Il modello suggerirebbe che la volatilità di oggi sia un indicatore della volatilità di domani e cioè che momenti a bassa volatilità sono seguiti da bassa volatilità e viceversa. Il problema dell’ARCH model è che esso può avere spesso delle oscillazioni di volatilità che danno al modello un comportamento a tratti esplosivo. Per ovviare a questo problema, aggiungiamo il parametro della volatilità sul giorno precedente, proprio come lo facevamo sul modello AR per ottenere ARMA.
L’inclusione della volatilità di ieri mi permette di smussare i comportamenti esplosivi del modello che si basano sul solo cambio di volatilità di un solo giorno (volatilità di oggi per domani) [4].
Dopo questa breve introduzione possiamo sviluppare un codice Python che ci permetta di risolvere il nostro problema, seguendo gli ormai noti 6 steps di programmazione.
STEP 1 – IMPORTAZIONE E LETTURA DATI
Assumiamo di aver importato tutte le librerie generiche (numpy, pandas, matplot) come già fatto nell’esempio precedente e delle funzioni di lettura dati (incluso yfinance e yf) per i valori di S&P500 negli ultimi due anni.
STEP 2 – ELABORAZIONE, TRASFORMAZIONE E ORGANIZZAZIONE DATI
A questo punto poiché vogliamo studiare e prevedere la volatilità del S&P500, lanciamo un’operazione.
returns = 100 * SP500.Close.pct_change().dropna()
plt.figure(figsize=(10,4))
plt.title(‘S&P500 Returns’)
plt.ylabel(‘% Return’)
plt.xlabel (‘Date’,alpha=1)
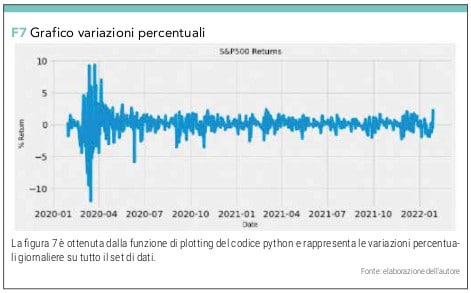
plt.plot(returns)
che invece di darci i valori assoluti giornalieri ci restituisce le variazioni percentuali in forma numerica (vedi figura 6) e grafica (vedi figura 7)
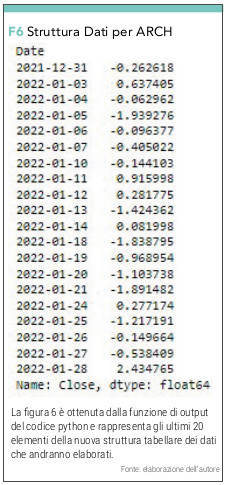
STEP 3 – DEFINIZIONE DEL MODELLO
Importiamo la libreria che ci permetterà di implementare il metodo ARCH
pip install arch
e le funzioni di Partial Autocorrelation e Autocorrelation che ci danno una prima indicazione dei valori di p e q da utilizzare per l’addestramento del modello:
from arch import arch_model
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
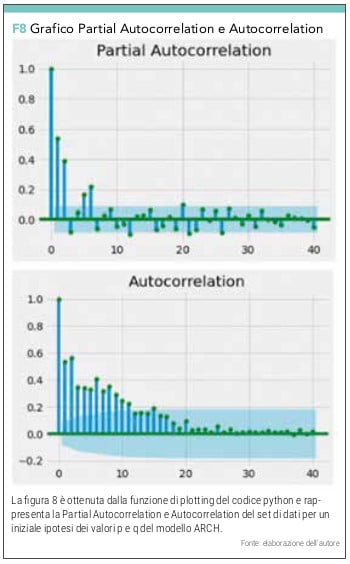
pacf = plot_pacf(returns**2, lags=40,color=’g’)
acf = plot_acf(returns**2, lags=40,color=’g’)
Dal grafico (vedi figura 8) possiamo cominciare a provare a calcolare la bontà del modello con varie combinazioni di p e q.
STEP 4 – ADDESTRAMENTO DEL MODELLO
Dopo vari tentativi per addestrare il modello scegliamo di procedere con i valori di p=2 e q=2.
model = arch_model(returns, p=2, q=2)
model_fit = model.fit()
A questo punto creiamo il test e train data set con la seguente serie di linee di codice:
rolling_predictions = []
test_size = 30*12
for i in range(test_size):
train = returns[:–(test_size–i)]
model = arch_model(train, p=2, q=2)
model_fit = model.fit(disp=‘off’)
pred = model_fit.forecast(horizon=1)
rolling_predictions.append(np.sqrt(pred.variance.values[–1,:][0]))
STEP 5 – VALUTAZIONE DELL’AFFIDABILITÀ DEL MODELLO
Passiamo alla valutazione grafica che otteniamo con:
plt.figure(figsize=(10,4))
true = plt.plot(returns[–30*12:])
preds = plt.plot(rolling_predictions)
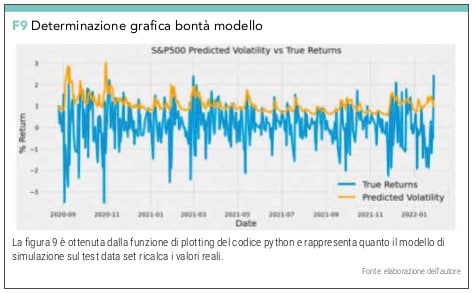
plt.title(‘S&P500 Volatility Prediction – Rolling Forecast’)
plt.legend([‘True Returns’, ‘Predicted Volatility’)
Con questi valori riusciamo ad ottenere un modello che pur non replicando perfettamente i valori reali riesce a bene identificare i suoi picchi (vedi figura 9).
STEP 6 – PREVISIONE
A questo punto e con questo modello, lanciamo la previsione di 7 giorni.
pred = model_fit.forecast(horizon=8)
future_dates = [returns.index[-1] + timedelta(days=i) for i in range(1,9)]
pred = pd.Series(np.sqrt(pred.variance.values[-1,:]), index=future_dates)
che con la funzione di plotting
plt.figure(figsize=(10,4))
plt.plot(pred)
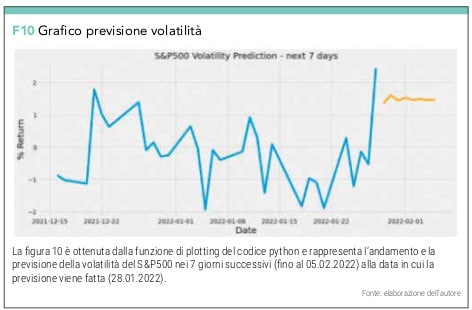
plt.title(‘S&P500 Volatility Prediction – Next 30 Days’, fontsize=20)
ci permette di visualizzare il grafico in figura 10 e il suo array in figura 11
Conclusioni
Per quanto la trattazione possa risultare mediamente complessa, lo studio rappresenta semplicemente un punto di partenza per approfondire la ricerca di modelli che possano aiutare il trader o l’investitore nelle sue scelte. In questi 3 modelli rappresentati finora le possibilità di settare i parametri sono notevoli ed ogni loro combinazione può dare risultati completamente diversi. In un mondo in cui combattiamo tra prospettive di inflazione e stagflazione sarebbe troppo semplificativo affidare i nostri risparmi a poche linee di codice. In tempi normali e su un orizzonte di lungo termine potremmo ancora pensare che il progresso, legato a doppio filo con la capacità di sviluppo di know how, e misurabile con il PIL, continui a sostenere i corsi azionari.
Tuttavia se da un lato la capacità di sviluppare innovazione è infinita (almeno cosi mi piace pensare) bisogna considerare attentamente che:
a) l’implementazione dell’innovazione a livello produttivo è comunque limitata. Si pensa che la capacità innovativa dell’essere umano tradotta in produttività, oscilli con valori medi annuali tra il 2% e il 3% al massimo;
b) in futuro avremo minore accesso alle risorse sia per la loro riducenda disponibilità sia per una crescente attenzione a forme di sostenibilità produttive. Dopo il Covid si sono moltiplicate teorie sulla decrescita, ridistribuzione di ricchezza e ricorrono sempre più spesso idee tipo “Great Reset”, “New Order” e così via.
Oggi siamo parte di un ecosistema dei mercati finanziari dove la lotta tra ipo e iper informazione ha mantenuto lo stesso livello di esposizione a bolle finanziarie [5], dove la quantità di strumenti derivati fornisce un ampio spettro di possibilità di investimento con posizioni long e altrettante short, dove il debito globale ha raggiunto livelli record, dove abbiamo ripetutamente fallito nella esasperata ricerca di un bene che incorpori il significato di valore (che sia l’oro, il petrolio o il bitcoin e similari), dove l’entropia dei nostri sistemi (geopolitici, demografici, ecologici e finanziari) accelera esponenzialmente. Tutto ciò per dire che le previsioni saranno sempre oggetto di trattazione a complessità crescente e gli algoritmi dovranno tenere in considerazione sempre più variabili. Nei prossimi numeri illustreremo altri algoritmi previsionali lasciando le serie temporali e utilizzando tecniche di previsione supportate da reti neurali.
Per chi fosse interessato ad ottenere i codici python completi e strutturati per un plug and play in ambiente Jupiter Notebook, richiedetelo pure all’autore all’indirizzo email nicola.matarese73@gmail.com.
-
I sei steps di un codice ML:
Importazione e lettura dati
Elaborazione, trasformazione e organizzazione dati
Definizione del modello da utilizzare
Addestramento del modello
Valutazione dell’affidabilità del modello
Previsione ↑ -
Il parametro m si riferisce al numero di osservazioni per ciclo stagionale.
Tipicamente, m corrisponde ad alcune periodicità ricorrenti come:
7 – giorni
12 – mensile
52 – settimanale
Analizzando il valore giornaliero per noi m=7 ↑ -
Numero di giorni da prevedere ↑
-
Lo studio sulla volatilità del S&P500 è un esempio di trasformazione dei valori di cui già parlato nelle premesse dello studio delle serie temporali. Possiamo affermare che l’S&P500 mentre non é stazionario nei suoi valori (in quanto soggetto ad un “trend”, lo é sulle differenze dei suoi valori. ↑
-
In un mercato efficiente non si creano squilibri. ↑
Nicola Matarese
Classe 1973, ha conseguito una laurea magistrale in ingegneria meccanica ed ha ricoperto ruoli manageriali all’interno di realtà industriali in ambito aerospazio e difesa. È appassionato di trading e opera sui mercati dal 2001. Da qualche anno lavora a sistemi di trading supportati da teorie sui Big Data e Intelligenza Artificiale.
